[BJ] 1206: DFS와 BFS(Java)

💡 문제

 

문제

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

입력

첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

출력

첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.

예제 입력 1

5 5 3
5 4
5 2
1 2
3 4
3 1

예제 출력 1

3 1 2 5 4
3 1 4 2 5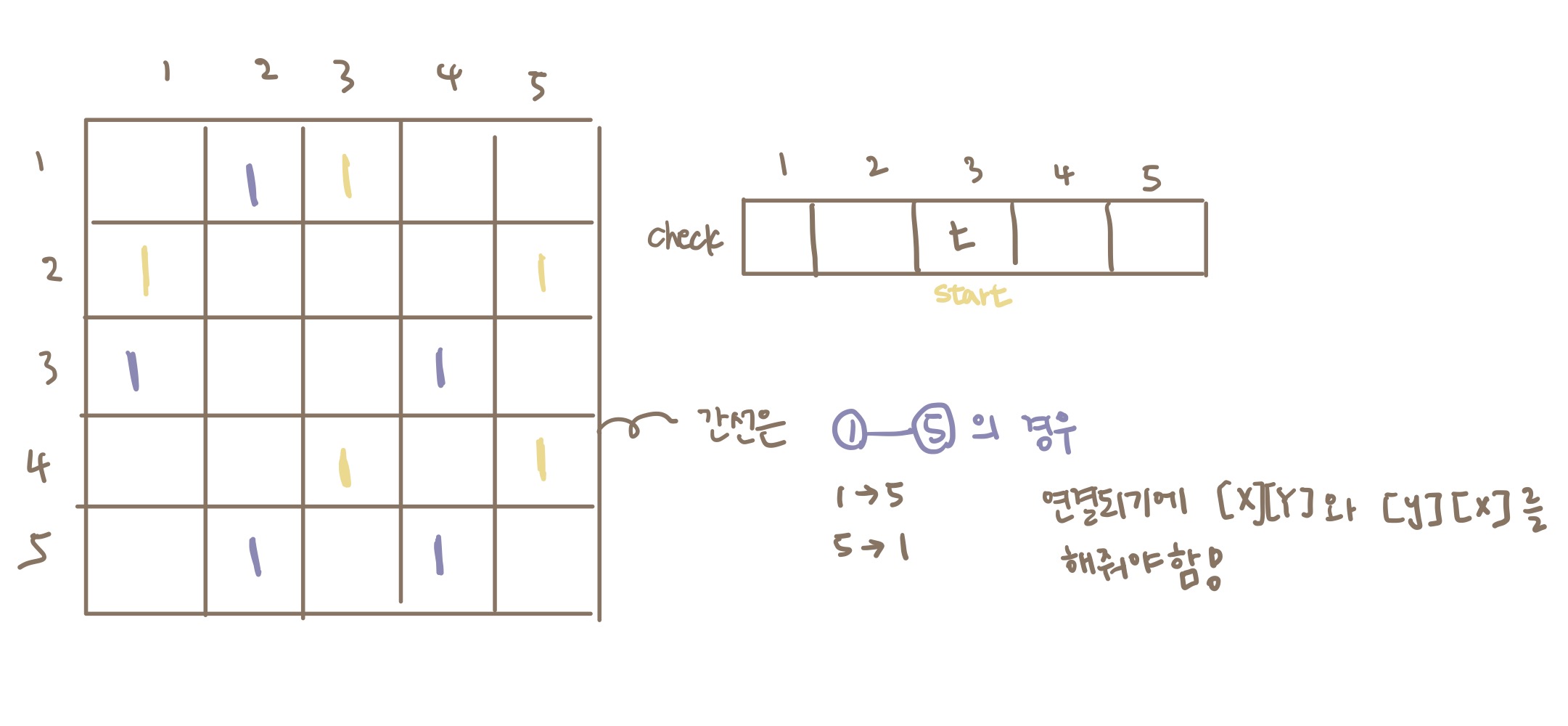

---

💡 접근 방법

---

🤦‍♀️ My Solution

package WS;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.Stack;
import java.util.StringTokenizer;

public class BJ_1260 {

    static int N, M, V;
    static int[][] link;
    static boolean[] check;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        V = Integer.parseInt(st.nextToken());
        link = new int[1001][1001];

        int x, y;
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            x = Integer.parseInt(st.nextToken());
            y = Integer.parseInt(st.nextToken());
            link[y][x] = link[x][y] = 1; // 간선 연결 상태

        }
        check = new boolean[1001];
        DFS();
        check = new boolean[1001];
        System.out.println();
        BFS();
    }

    static void BFS() {
        Queue<Integer> que = new ArrayDeque<>();
        que.add(V);// 시작점 넣음
        check[V] = true;
        System.out.print(V + " "); // 시작점 출력

        while (!que.isEmpty()) { // 큐가 비어있지 않을때까지
            int node = que.poll(); // 맨처음: 시작값을 꺼내옴

            for (int i = 1; i <= N; i++) {
                if (link[i][node] == 1 && check[i] == false) {
                    que.add(i);
                    System.out.print(i + " ");
                    check[i] = true;
                }

            }
        }

    }

    static void DFS() {
        Stack<Integer> que = new Stack<>();
        que.push(V);// 시작점 넣음

        while (!que.isEmpty()) { // 큐가 비어있지 않을때까지
            int node = que.pop(); // 맨처음: 시작값을 꺼내옴
            if (check[node])
                continue;
            check[node] = true;
            System.out.print(node + " ");

            for (int i = N; i >= 1; i--) {
                if (link[i][node] == 1 && check[i] == false) {
                    que.push(i);

                }
            }
        }

    }
}

---

참고: https://m.blog.naver.com/lm040466/221787478911